If the coefficients of the series representation of a hypergeometric function are
rational functions of the summation index, then the hypergeometric function can be
expressed as a linear sum of Lerch
Further, if the parameters of the hypergeometric function are rational, we can proceed to express the hypergeometric function as a linear sum of polylogarithms. The polylogarithm function is defined by
The first theorem shows how to express such a hypergeometric function as a linear
sum of Lerch
Theorem
Let
have partial fraction decomposition
Then
The next theorem can be used to range reduce the third argument of a Lerch
Theorem
The next two theorems show how to convert Lerch
Theorem
Theorem
Let
Corollary
Let
where
|
|
|
Lerch Phi and Polylogarithms
|
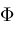 functions. The Lerch
functions. The Lerch



 ,
,
 , and
, and



 .
.






 and
and
 . Then
. Then






