The algorithm in this paper promises to return all solutions of an equation
 over an interval
over an interval
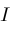 . The generalization to two dimensions does the same in two dimensions and we
are confident the same method can be generalized to . The generalization to two dimensions does the same in two dimensions and we
are confident the same method can be generalized to
 dimensions.
dimensions.
Computer algebra is moving out of the era where symbolic expressions like
 , ,
 , Maple's RootOf, and Mathematica's InverseFunction have had poor or no relation to
actual numbers into an era where proper semantics establishing a mapping from symbolic
expressions to complex numbers is fully appreciated and enforced. Symbolic expressions
are names for numbers. In this paper, we introduce a new kind of name, the Nonlin()
object. Rather than a vague unknown solution of a nonlinear equation (cf. Mathematica's
InverseFunction), a Nonlin() object represents a particular number which can be evaluated
to as many decimal places as the user likes, just as it is possible to do with Pi
or E. The future promises to bring more such objects into the realm of computer
algebra: implicit functions, implicit solutions of differential equations, etc., and
such objects will always have a definite meaning over the field of complex numbers.
The mathematical impetus to study the algebra of such objects more carefully will
likely emerge as these objects come on line, can be routinely calculated, and are
equipped with sensible semantics. , Maple's RootOf, and Mathematica's InverseFunction have had poor or no relation to
actual numbers into an era where proper semantics establishing a mapping from symbolic
expressions to complex numbers is fully appreciated and enforced. Symbolic expressions
are names for numbers. In this paper, we introduce a new kind of name, the Nonlin()
object. Rather than a vague unknown solution of a nonlinear equation (cf. Mathematica's
InverseFunction), a Nonlin() object represents a particular number which can be evaluated
to as many decimal places as the user likes, just as it is possible to do with Pi
or E. The future promises to bring more such objects into the realm of computer
algebra: implicit functions, implicit solutions of differential equations, etc., and
such objects will always have a definite meaning over the field of complex numbers.
The mathematical impetus to study the algebra of such objects more carefully will
likely emerge as these objects come on line, can be routinely calculated, and are
equipped with sensible semantics.
|