From calculus we know that if
 then
then
 
for some
 . If . If
 for all
for all
 and
and
 , then , then
 for all
for all
 where
where
 . Thus, while searching for zeros of . Thus, while searching for zeros of
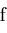 on
on
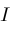 , we can eliminate all of , we can eliminate all of
 from consideration if we know
from consideration if we know
 and a finite bound
and a finite bound
 . If interval . If interval
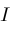 is sufficiently small, then
is sufficiently small, then
 will determine a finite bound
will determine a finite bound
 on
on
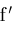 . This leads to procedure
Narrow( . This leads to procedure
Narrow(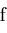 , ,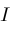 ) which trims the ends of interval ) which trims the ends of interval
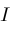 by this technique before calling
Zeros
(if it must). The recursive calls in
Zeros
are changed to be calls to procedure
Narrow.
by this technique before calling
Zeros
(if it must). The recursive calls in
Zeros
are changed to be calls to procedure
Narrow.
We change lines 13 and 19-20 of procedure Zeros to be:

 return
Narrow return
Narrow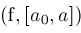
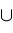 Narrow
Narrow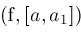 ; ;

 return
Narrow
return
Narrow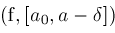
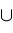
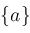



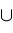 Narrow
Narrow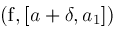 ; ;
and add procedure Narrow below:
proc
Narrow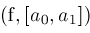
 ; ;
if
 then
then
 for
for
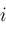 from
from
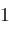 to
to
 do
do


 ; ;


 ; ;

 if
if
 then
then


 return
return
 ; ;

 fi;
fi;
 od;
od;
fi;
return
Zeros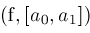 ; ;
proc
Bound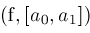
 ; ;
return
 ; ;
 is a "fudge factor" which we currently set as
is a "fudge factor" which we currently set as
 . .
|
 then
then

 . If
. If
 for all
for all
 and
and
 , then
, then
 for all
for all
 where
where
 . Thus, while searching for zeros of
. Thus, while searching for zeros of
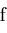 on
on
 , we can eliminate all of
, we can eliminate all of
 from consideration if we know
from consideration if we know
 . If interval
. If interval
 will determine a finite bound
will determine a finite bound
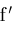 . This leads to procedure
Narrow(
. This leads to procedure
Narrow(
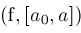
 Narrow
Narrow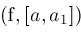 ;
;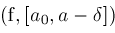
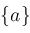
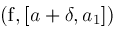 ;
;
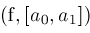
 ;
; then
then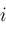 from
from
 to
to
 do
do ;
; ;
; then
then ;
; ;
; ;
;
 .
.