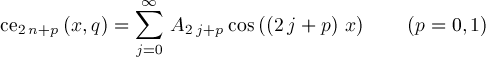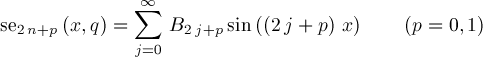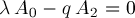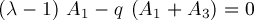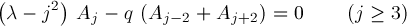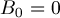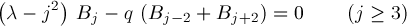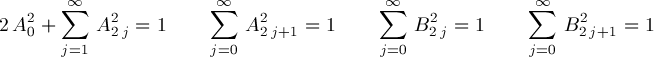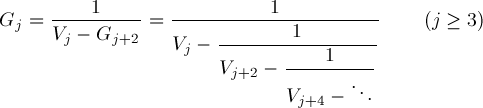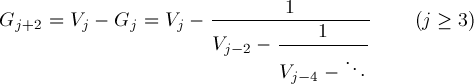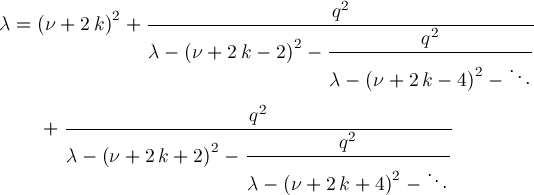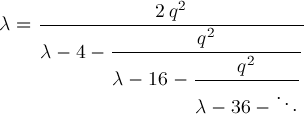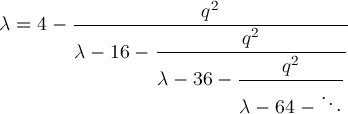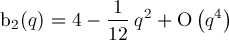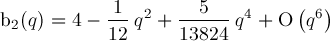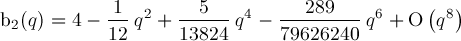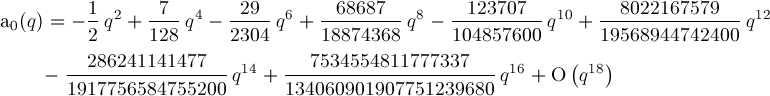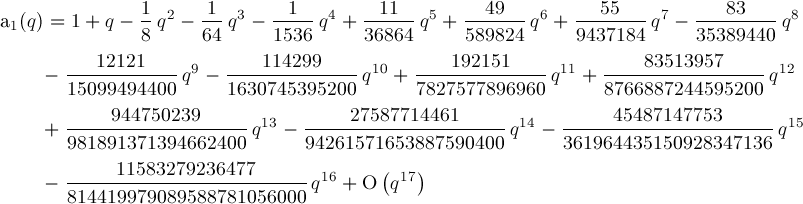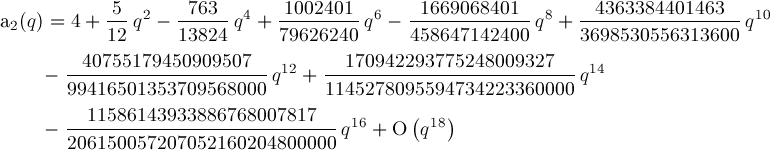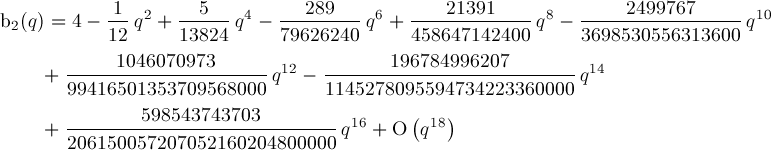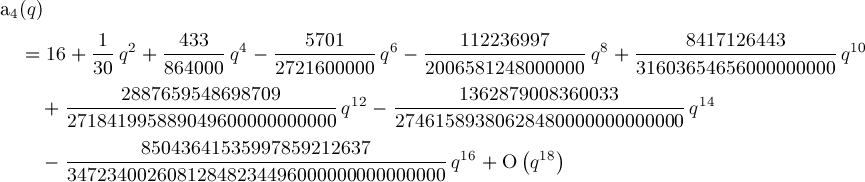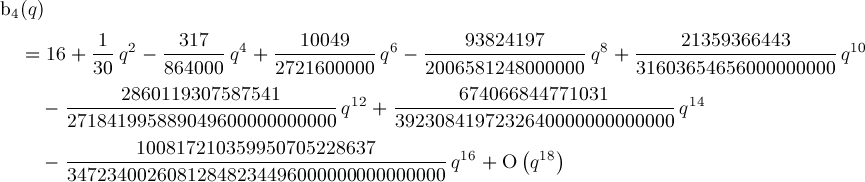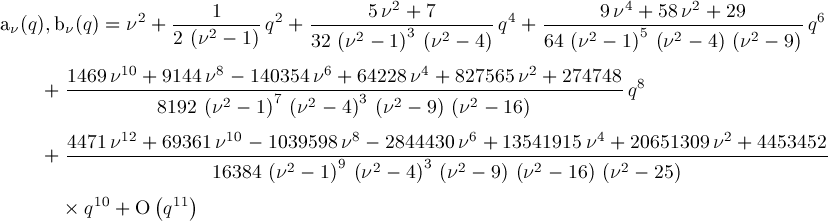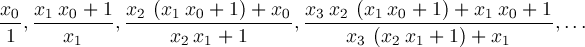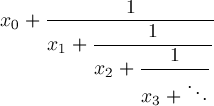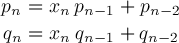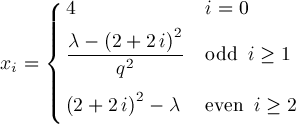Greetings PLANETQUANTUM.COM visitor. Today we discuss Mathieu function eigenvalue formulas.

Mathieu Functions

Mathieu functions

are periodic solutions of differential equation

having periods π and 2π for p=0 and p=1 respectively. Even solutions ce_ν(x,q) (ν=0,1,2,...) and odd solutions se_ν(x,q) (ν=1,2,...) correspond to countably many eigenvalues λ(q)=a_ν(q) and b_ν(q) respectively. Additionally, a_ν(q) and b_ν(q)=ν²+O(q) for q near 0 . The coefficients A_j and B_j satisfy recurrences

It is also usual to apply one of the normalization conditions

Continued Fractions Involving λ

Let

The A_j recurrences of the preceding section lead to

Further considerations get Wang & Guo p621 formula (3)

Letting ν=0 and k=0 gets Wang & Guo p621 formula (4)

for even ν period π solutions. Another observation gets Wang & Guo p621 formula (5)

We like to use formula (5) to compute b₂(q). From formula (5), we see b₂(q)=4+O(q^2) for small q. Substituting λ=4+O(q^2) into the RHS of formula (5) gets

Iterating gets better approximations:

The procedure is automated in MathieuFormulaB2.q.txt. Using MathieuFormulaB2.q.txt and similar code, we can derive formulas for a_ν(q) and b_ν(q) when ν≤10 .

We use Wang & Guo p621 (3), p623 (8), p623 (11), p621 (5), and p627 (7) to compute a_ν(q) for even ν≥0, a₁(q) and b₁(q), a_ν(q) and b_ν(q) for odd ν≥3, b₂(q), and b_ν(q) for even ν≥4, respectively. For brevity, we omit detailing these cases. Some typos discovered on Wang & Guo p623 are mentioned in our MathieuFormulaB2.q.txt code comments.

Formulas for a_ν(q) and b_ν(q) when ν≤10

The following formulas we've generated may be compared with Abramowitz & Stegun p724 20.2.25, Wang & Guo pp628-629 (4), and NIST 28.6.1-13 (see References):

Formula for a₀(q):

Formula for a₁(q):

Formula b₁(q)=a₁(-q).

Formula for a₂(q):

Formula for b₂(q):

Formula for a₃(q):

Formula b₃(q)=a₃(-q).

Formula for a₄(q):

Formula for b₄(q):

Formula for a₅(q):

Formula b₅(q)=a₅(-q).

Formula for a₆(q):

Formula for b₆(q):

Formula for a₇(q):

Formula b₇(q)=a₇(-q).

Formula for a₈(q):

Formula for b₈(q):

Formula for a₉(q):

Formula b₉(q)=a₉(-q).

Formula for a₁₀(q):

Formula for b₁₀(q):

We've placed these formulas in text form in News170314.q.txt .

Formula for a_ν(q) and b_ν(q) when ν≥11

We can also generate general formulas for symbolic ν≥N where N can take on various concrete values. The next formula may be compared with Abramowitz & Stegun p724 20.2.26, Wang & Guo p629 (5), and NIST 28.6.14 (see References). The formula does not imply a_ν(q)=b_ν(q), just a_ν(q)=b_ν(q)+O(q¹¹).

Formula for a_ν(q) and b_ν(q) when ν≥11:

_FloatMathieuEigenB2

Let's describe a function FloatMathieuEigenB2 for computing b₂(q) using continued fraction convergents. In general, numerators p_n and denominators q_n of successive convergents p_n/q_n

of a continued fraction

satisfy recurrence relations

Letting

gets us a numerical implementation of Wang & Guo p621 formula (5). Starting with small q and initial approximation λ=4 for b₂(q), repeatedly applying Wang & Guo p621 formula (5) gives increasingly better approximations converging to b₂(q). We've implemented this theory by two functions _FloatMathieuEigenB2 and _FloatMathieuEigenB2Step in FloatMathieuEigenB2.q.txt. Let's try it out.

>(MathieuB 2 0.5)
3.979189215751358
>(Eval (Subst 'q 0.5 b2))
3.979189215751358
>(MathieuB 2 5.)
2.099460445486666
>(Eval (Subst 'q 5. b2))
2.099593807819844
>(SetPrecision 3000)
3000
>(MathieuB 2 5.)
2.09946044548666536395565456881965731303214394331170320017824203\
0096910666016096613169463818290910455650222866107481368603826818\
2200885982391039191016922951691897213446342709546044123319893224\
4884779534875094432194561990996001898932313100168622128963566755\
2444799315475114167572014411096483980218759337156610966126207955\
3363964379976071374935610048542924550102678732839474622165336383\
0067067482178047952633487575457431874307824633234823151409436199\
8786873010088485494067402909622972233594584633679500216364218960\
6063396454077401028375665634968944833812045262700930370779049038\
3793978604457590588170909146959619599196244413809076892648159886\
1957883688707095515970390508393946463490626842421943592404583448\
0864433781550131376210228929628763001849675083051023805804201152\
1601438315610853345308704126733916766040169171274208341403528809\
6696506658587696813249633857942585672721678187404117233059374475\
73677448

Abramowitz & Stegun p749 (Table 20.1) gives b₂(5.)=2.09946045  .

_FloatMathieuSe

Let's use the eigenvalue (MathieuB 2 0.5) just computed to compute (MathieuSe 2 1. 0.5) . Here is what we get:

>(MathieuSe 2 1. 0.5)
.93979586513485
>(SetPrecision 3000)
3000
>(MathieuSe 2 1. 0.5)
.939795865134850041321678599481074546543262353406214114560268136\
8196540239619884690957002732827552779069837332177149621585041116\
8976798645480024426901215984830593452983662685294768303657473252\
0860218992214922224741591366430370338480542298581534202903552027\
6988366636597377708410528576564072790075734001941052307653142850\
5642983542365998686172741582862899971992421575398112553164272012\
9006459367958829277619106068329006366963204110893091488526396115\
0577894100844961888405895444155032836355894314832703732934114758\
6294014368835133940117757556488032470930881996175776298583883469\
6472818571577806083454535926227921179828255195281776622581385055\
7925365840943668310034904112549202367394490044685600574045069700\
1583455641555883218733669121664335272259948510014873224908867258\
7848789167852035522487911323779219510079541420879518183739450766\
7322680801736431603890146945988466236317979940666868486905042518\
39762175

We put additional details of this calculation and some source code in MathieuSeTrace.txt and FloatMathieuSe.q.txt

Conclusion

We've discussed Mathieu functions ce_ν(x,q) and se_ν(x,q), continued fractions involving Mathieu function eigenvalues λ(q)=a_ν(q) and b_ν(q), formulas for a_ν(q) and b_ν(q) for small q, a numerical method for computing eigenvalues via continued fraction convergents, and illustrating calculations of (MathieuB 2 0.5), (MathieuB 2 5.), and (MathieuSe 2 1. 0.5).

We might cover calculating Mathieu Functions for large q in a future post.

References

Arthur Erdélyi, ed., (1955) CHAPTER XVI MATHIEU FUNCTIONS, SPHEROIDAL, AND ELLIPSOIDAL WAVE FUNCTIONS, Higher Transcendental Functions, Volume III, Robert E. Krieger Publishing Company, Malabar, Florida.

Milton Abramowitz and Irene A. Stegun, eds. (1965) 20. Mathieu Functions, HANDBOOK OF MATHEMATICAL FUNCTIONS with Formulas, Graphs, and Mathematical Tables, Dover Publications, Inc.

F. W. J. Olver, A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, and B. V. Saunders, eds. (2016) 28.6 Expansions for Small q, NIST Digital Library of Mathematical Functions, Release 1.0.14 of 2016-12-21.

Z. X. Wang and D. R. Guo, (1989) Chapter 12: MATHIEU FUNCTIONS, Special Functions, World Scientific Publishing Co Pte Ltd.

Wikipedia Contributors, (2017) Continued fraction, Infinite continued fractions and convergents, Wikipedia, The Free Encyclopedia.

Wikipedia Contributors, (2017) Mathieu function, Wikipedia, The Free Encyclopedia.

Source Code: News170314.q.txt , MathieuFormulaB2.q.txt , FloatMathieuEigenB2.q.txt , MathieuSeTrace.txt , and FloatMathieuSe.q.txt .