The preceding algorithm has been implemented in Maple and run on various inputs including the following examples:
Figures 1.1-1.2 picture these two functions.
The operations of procedures
Zeros
and
Narrow
are represented in
Figures 2.1-2.2. Each right triangle represents a narrowing step by procedure Narrow.
A triangle with vertices
The effects of procedure
Gaps on the z-axis between the triangles (most visible in
Figure 2.2), represent procedures
Locate
and
Newton
taking over from procedures
Zeros
and
Narrow
to locate an isolated root of
In Maple, we choose nsolve as the name of the main routine to resemble Maple's routine fsolve. Procedure nsolve returns Nonlin() objects and these, like E or Pi, can be evaluated via Maple's evalf to as many decimal places as desired. Thus,
Each Nonlin() object records the nonlinear equation which is solved, the Newton iteration
formula, a bounding interval for the root, and the two bounds
|
|
|
Results
|
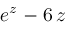
 for
for
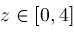
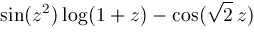
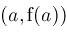 ,
,
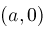 ,
,
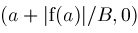 represents
Narrow
detecting
represents
Narrow
detecting
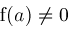 and
and
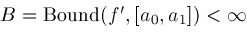 allowing
Narrow
to eliminate subinterval
allowing
Narrow
to eliminate subinterval
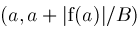 as a possible location for any zeros of
as a possible location for any zeros of
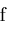 .
.
 can be seen wherever there is a change in the slope of the hypotenuses of the triangles
or two right triangles' altitudes merge together.
can be seen wherever there is a change in the slope of the hypotenuses of the triangles
or two right triangles' altitudes merge together.
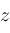 -axes where the roots are located.
-axes where the roots are located.
 needed by procedure Newton to terminate properly.
needed by procedure Newton to terminate properly.